GEOMETRIA ANALÍTICA
Encontre a medida dos semieixos, os focos e a excentricidade da hipérbole x2 - 4y2 + 16 = 0.
a=4; b=4; F1(0, -2√5) e F2(0, 2√5); e=√2
a=4; b=16; F1(0, -2√5) e F2(0, -2√5); e=√5
a=2; b=4; F1(0, -2√5) e F2(0, 2√5); e=√5
a=2; b=2; F1(0, -2√5) e F2(0, 2√5); e=√3
a=4; b=16; F1(0, 2√5) e F2(0, 2√5); e=√5
Determine respectivamente os valores de a e b para que os pontos A (2, a, 3), B (2, 1, - 5) e C (b, -3, 4) sejam colineares.
O planejamento de um bairro de uma cidade com grande expansão populacional foi feito considerando uma região plana, com quadras de mesma dimensão sendo delimitadas por ruas paralelas e perpendiculares. O esboço desse projeto foi realizado e feita uma representação do bairro no plano cartesiano localizando-o no segundo quadrante, no qual as distâncias nos eixos coordenados são consideradas em quilômetros, conforme figura exposta a seguir.
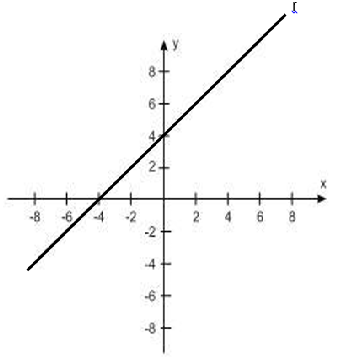
O percurso de uma linha de transporte coletivo que atravessará o bairro e outras regiões da cidade é representado pela reta r. Considere que no ponto P1 de coordenadas (-5,5) localiza-se um hospital universitário público e no ponto P2 , de coordenadas (x,y), um ponto de transporte coletivo. Assinale a alternativa que expressa a localização de P2 de forma que sua distância em relação ao hospital, medida em linha reta, não seja maior que 5 km e a equação que representa a reta r.
P2 (-3, 1), r: y=x+4.
P2 (0,4), r: y=x-4.
P2 (-3, 1), r: y=-x+4.
P2 (-5, 0), r: y=x+4.
P2 (2, 6), r: y=x+4.
O ponto médio do segmento definido pelos pontos A(2, -5) e B(-2,-3) é o centro de uma circunferência
. Considerando que o raio de seja igual a 2, assinale a alternativa que contém a sua equação reduzida.
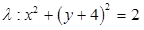
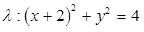
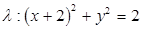
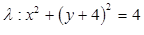
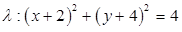
Assinale a alternativa que representa as equações paramétricas da reta que passa pelos pontos A(1,-1,2) e B(2,1,0)
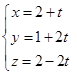
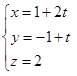
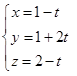
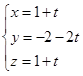
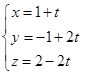
O vetor u=(-1,-1,-2) tem angulação de 60º com o vetor MN definido pelos pontos M(0,3,4) e N( x,-1,2). Com base no exposto, o valor de x está representado na alternativa
x= –34 ou x=-2
x= 34 ou x=2
x= –30 ou x=2
x= –34 ou x=2
x= –34 ou x=3
Um triângulo é determinado pelos pontos A (0,0), B (5,4) e C (3,8) do plano cartesiano com duas dimensões, x e y. Com base no exposto a sua área, em unidades de área, é igual a
28 u.a.
14 u.a.
26 u.a.
16 u.a.
18 u.a.
Determine uma equação geral do plano π determinado pelos pontos de coordenadas A(1, 1, 1), B(-1, -1, 5) e C(1, 2,-2) e assinale a alternativa correta.
4x – 6y – 2z + 6 = 0
2x + 6y + 2z = - 6
4x - 6y + 2z - 6 = 0
2x – 6y – 2z + 6 = 0
2x + 6y - 2z = 6
Uma empresa de produtos de limpeza implantou uma nova embalagem de cápsulas esféricas para comercializar o sabão líquido para lavar roupas. Considerando que o raio dessa cápsula seja igual a 1 cm, qual será o volume aproximado de sabão líquido presente em cada uma?
a=4; b=4; F1(0, -2√5) e F2(0, 2√5); e=√2
a=4; b=16; F1(0, -2√5) e F2(0, -2√5); e=√5
a=2; b=4; F1(0, -2√5) e F2(0, 2√5); e=√5
a=2; b=2; F1(0, -2√5) e F2(0, 2√5); e=√3
a=4; b=16; F1(0, 2√5) e F2(0, 2√5); e=√5
Determine respectivamente os valores de a e b para que os pontos A (2, a, 3), B (2, 1, - 5) e C (b, -3, 4) sejam colineares.
O planejamento de um bairro de uma cidade com grande expansão populacional foi feito considerando uma região plana, com quadras de mesma dimensão sendo delimitadas por ruas paralelas e perpendiculares. O esboço desse projeto foi realizado e feita uma representação do bairro no plano cartesiano localizando-o no segundo quadrante, no qual as distâncias nos eixos coordenados são consideradas em quilômetros, conforme figura exposta a seguir.
O percurso de uma linha de transporte coletivo que atravessará o bairro e outras regiões da cidade é representado pela reta r. Considere que no ponto P1 de coordenadas (-5,5) localiza-se um hospital universitário público e no ponto P2 , de coordenadas (x,y), um ponto de transporte coletivo. Assinale a alternativa que expressa a localização de P2 de forma que sua distância em relação ao hospital, medida em linha reta, não seja maior que 5 km e a equação que representa a reta r.
P2 (-3, 1), r: y=x+4.
P2 (0,4), r: y=x-4.
P2 (-3, 1), r: y=-x+4.
P2 (-5, 0), r: y=x+4.
P2 (2, 6), r: y=x+4.
O ponto médio do segmento definido pelos pontos A(2, -5) e B(-2,-3) é o centro de uma circunferência . Considerando que o raio de seja igual a 2, assinale a alternativa que contém a sua equação reduzida.
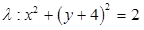
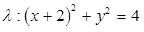
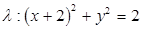
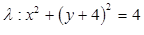
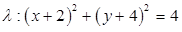
Assinale a alternativa que representa as equações paramétricas da reta que passa pelos pontos A(1,-1,2) e B(2,1,0)
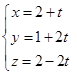
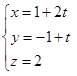
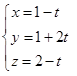
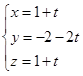
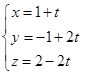
O vetor u=(-1,-1,-2) tem angulação de 60º com o vetor MN definido pelos pontos M(0,3,4) e N( x,-1,2). Com base no exposto, o valor de x está representado na alternativa
x= –34 ou x=-2
x= 34 ou x=2
x= –30 ou x=2
x= –34 ou x=2
x= –34 ou x=3
Um triângulo é determinado pelos pontos A (0,0), B (5,4) e C (3,8) do plano cartesiano com duas dimensões, x e y. Com base no exposto a sua área, em unidades de área, é igual a
28 u.a.
14 u.a.
26 u.a.
16 u.a.
18 u.a.
Determine uma equação geral do plano π determinado pelos pontos de coordenadas A(1, 1, 1), B(-1, -1, 5) e C(1, 2,-2) e assinale a alternativa correta.
4x – 6y – 2z + 6 = 0
2x + 6y + 2z = - 6
4x - 6y + 2z - 6 = 0
2x – 6y – 2z + 6 = 0
2x + 6y - 2z = 6
Uma empresa de produtos de limpeza implantou uma nova embalagem de cápsulas esféricas para comercializar o sabão líquido para lavar roupas. Considerando que o raio dessa cápsula seja igual a 1 cm, qual será o volume aproximado de sabão líquido presente em cada uma?
O planejamento de um bairro de uma cidade com grande expansão populacional foi feito considerando uma região plana, com quadras de mesma dimensão sendo delimitadas por ruas paralelas e perpendiculares. O esboço desse projeto foi realizado e feita uma representação do bairro no plano cartesiano localizando-o no segundo quadrante, no qual as distâncias nos eixos coordenados são consideradas em quilômetros, conforme figura exposta a seguir.
O percurso de uma linha de transporte coletivo que atravessará o bairro e outras regiões da cidade é representado pela reta r. Considere que no ponto P1 de coordenadas (-5,5) localiza-se um hospital universitário público e no ponto P2 , de coordenadas (x,y), um ponto de transporte coletivo. Assinale a alternativa que expressa a localização de P2 de forma que sua distância em relação ao hospital, medida em linha reta, não seja maior que 5 km e a equação que representa a reta r.
P2 (-3, 1), r: y=x+4.
P2 (0,4), r: y=x-4.
P2 (-3, 1), r: y=-x+4.
P2 (-5, 0), r: y=x+4.
P2 (2, 6), r: y=x+4.
O ponto médio do segmento definido pelos pontos A(2, -5) e B(-2,-3) é o centro de uma circunferência . Considerando que o raio de seja igual a 2, assinale a alternativa que contém a sua equação reduzida.
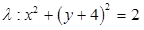
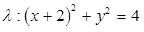
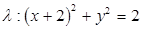
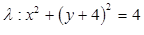
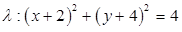
Assinale a alternativa que representa as equações paramétricas da reta que passa pelos pontos A(1,-1,2) e B(2,1,0)
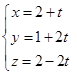
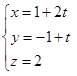
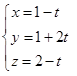
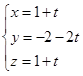
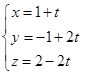
O vetor u=(-1,-1,-2) tem angulação de 60º com o vetor MN definido pelos pontos M(0,3,4) e N( x,-1,2). Com base no exposto, o valor de x está representado na alternativa
x= –34 ou x=-2
x= 34 ou x=2
x= –30 ou x=2
x= –34 ou x=2
x= –34 ou x=3
Um triângulo é determinado pelos pontos A (0,0), B (5,4) e C (3,8) do plano cartesiano com duas dimensões, x e y. Com base no exposto a sua área, em unidades de área, é igual a
28 u.a.
14 u.a.
26 u.a.
16 u.a.
18 u.a.
Determine uma equação geral do plano π determinado pelos pontos de coordenadas A(1, 1, 1), B(-1, -1, 5) e C(1, 2,-2) e assinale a alternativa correta.
4x – 6y – 2z + 6 = 0
2x + 6y + 2z = - 6
4x - 6y + 2z - 6 = 0
2x – 6y – 2z + 6 = 0
2x + 6y - 2z = 6
Uma empresa de produtos de limpeza implantou uma nova embalagem de cápsulas esféricas para comercializar o sabão líquido para lavar roupas. Considerando que o raio dessa cápsula seja igual a 1 cm, qual será o volume aproximado de sabão líquido presente em cada uma?
P2 (-3, 1), r: y=x+4.
P2 (0,4), r: y=x-4.
P2 (-3, 1), r: y=-x+4.
P2 (-5, 0), r: y=x+4.
P2 (2, 6), r: y=x+4.
O ponto médio do segmento definido pelos pontos A(2, -5) e B(-2,-3) é o centro de uma circunferência . Considerando que o raio de seja igual a 2, assinale a alternativa que contém a sua equação reduzida.
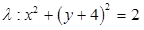
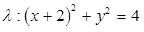
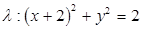
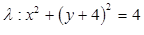
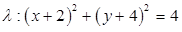
Assinale a alternativa que representa as equações paramétricas da reta que passa pelos pontos A(1,-1,2) e B(2,1,0)
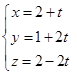
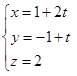
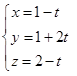
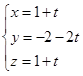
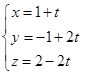
O vetor u=(-1,-1,-2) tem angulação de 60º com o vetor MN definido pelos pontos M(0,3,4) e N( x,-1,2). Com base no exposto, o valor de x está representado na alternativa
x= –34 ou x=-2
x= 34 ou x=2
x= –30 ou x=2
x= –34 ou x=2
x= –34 ou x=3
Um triângulo é determinado pelos pontos A (0,0), B (5,4) e C (3,8) do plano cartesiano com duas dimensões, x e y. Com base no exposto a sua área, em unidades de área, é igual a
28 u.a.
14 u.a.
26 u.a.
16 u.a.
18 u.a.
Determine uma equação geral do plano π determinado pelos pontos de coordenadas A(1, 1, 1), B(-1, -1, 5) e C(1, 2,-2) e assinale a alternativa correta.
4x – 6y – 2z + 6 = 0
2x + 6y + 2z = - 6
4x - 6y + 2z - 6 = 0
2x – 6y – 2z + 6 = 0
2x + 6y - 2z = 6
Uma empresa de produtos de limpeza implantou uma nova embalagem de cápsulas esféricas para comercializar o sabão líquido para lavar roupas. Considerando que o raio dessa cápsula seja igual a 1 cm, qual será o volume aproximado de sabão líquido presente em cada uma?
Assinale a alternativa que representa as equações paramétricas da reta que passa pelos pontos A(1,-1,2) e B(2,1,0)
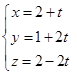
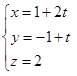
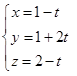
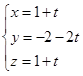
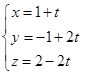
O vetor u=(-1,-1,-2) tem angulação de 60º com o vetor MN definido pelos pontos M(0,3,4) e N( x,-1,2). Com base no exposto, o valor de x está representado na alternativa
x= –34 ou x=-2
x= 34 ou x=2
x= –30 ou x=2
x= –34 ou x=2
x= –34 ou x=3
Um triângulo é determinado pelos pontos A (0,0), B (5,4) e C (3,8) do plano cartesiano com duas dimensões, x e y. Com base no exposto a sua área, em unidades de área, é igual a
28 u.a.
14 u.a.
26 u.a.
16 u.a.
18 u.a.
Determine uma equação geral do plano π determinado pelos pontos de coordenadas A(1, 1, 1), B(-1, -1, 5) e C(1, 2,-2) e assinale a alternativa correta.
4x – 6y – 2z + 6 = 0
2x + 6y + 2z = - 6
4x - 6y + 2z - 6 = 0
2x – 6y – 2z + 6 = 0
2x + 6y - 2z = 6
Uma empresa de produtos de limpeza implantou uma nova embalagem de cápsulas esféricas para comercializar o sabão líquido para lavar roupas. Considerando que o raio dessa cápsula seja igual a 1 cm, qual será o volume aproximado de sabão líquido presente em cada uma?
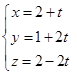
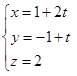
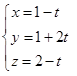
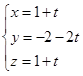
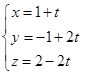
O vetor u=(-1,-1,-2) tem angulação de 60º com o vetor MN definido pelos pontos M(0,3,4) e N( x,-1,2). Com base no exposto, o valor de x está representado na alternativa
x= –34 ou x=-2
x= 34 ou x=2
x= –30 ou x=2
x= –34 ou x=2
x= –34 ou x=3
Um triângulo é determinado pelos pontos A (0,0), B (5,4) e C (3,8) do plano cartesiano com duas dimensões, x e y. Com base no exposto a sua área, em unidades de área, é igual a
28 u.a.
14 u.a.
26 u.a.
16 u.a.
18 u.a.
Determine uma equação geral do plano π determinado pelos pontos de coordenadas A(1, 1, 1), B(-1, -1, 5) e C(1, 2,-2) e assinale a alternativa correta.
4x – 6y – 2z + 6 = 0
2x + 6y + 2z = - 6
4x - 6y + 2z - 6 = 0
2x – 6y – 2z + 6 = 0
2x + 6y - 2z = 6
Uma empresa de produtos de limpeza implantou uma nova embalagem de cápsulas esféricas para comercializar o sabão líquido para lavar roupas. Considerando que o raio dessa cápsula seja igual a 1 cm, qual será o volume aproximado de sabão líquido presente em cada uma?
x= –34 ou x=-2
x= 34 ou x=2
x= –30 ou x=2
x= –34 ou x=2
x= –34 ou x=3
Um triângulo é determinado pelos pontos A (0,0), B (5,4) e C (3,8) do plano cartesiano com duas dimensões, x e y. Com base no exposto a sua área, em unidades de área, é igual a
28 u.a.
14 u.a.
26 u.a.
16 u.a.
18 u.a.
Determine uma equação geral do plano π determinado pelos pontos de coordenadas A(1, 1, 1), B(-1, -1, 5) e C(1, 2,-2) e assinale a alternativa correta.
4x – 6y – 2z + 6 = 0
2x + 6y + 2z = - 6
4x - 6y + 2z - 6 = 0
2x – 6y – 2z + 6 = 0
2x + 6y - 2z = 6
Uma empresa de produtos de limpeza implantou uma nova embalagem de cápsulas esféricas para comercializar o sabão líquido para lavar roupas. Considerando que o raio dessa cápsula seja igual a 1 cm, qual será o volume aproximado de sabão líquido presente em cada uma?
28 u.a.
14 u.a.
26 u.a.
16 u.a.
18 u.a.
Determine uma equação geral do plano π determinado pelos pontos de coordenadas A(1, 1, 1), B(-1, -1, 5) e C(1, 2,-2) e assinale a alternativa correta.
4x – 6y – 2z + 6 = 0
2x + 6y + 2z = - 6
4x - 6y + 2z - 6 = 0
2x – 6y – 2z + 6 = 0
2x + 6y - 2z = 6
Uma empresa de produtos de limpeza implantou uma nova embalagem de cápsulas esféricas para comercializar o sabão líquido para lavar roupas. Considerando que o raio dessa cápsula seja igual a 1 cm, qual será o volume aproximado de sabão líquido presente em cada uma?
4x – 6y – 2z + 6 = 0
2x + 6y + 2z = - 6
4x - 6y + 2z - 6 = 0
2x – 6y – 2z + 6 = 0
2x + 6y - 2z = 6